『ルビィのぼうけん』勝手に超訳 Vol.05

引き続き、４章です。

ペンギンたちが登場するこの章では、不思議な言葉を話すペンギンとのやりとりを通じて

３つのことを伝えようとしている、という話を前回書きました。

今回は３つめの

お互いが理解できる程度まで分解して

間違いなく曖昧でない形で定義しなければいけない

について説明します。

本の後半にある大人向けの解説を読んでいると

「データ構造」

という言葉が登場します。

そして、データ構造とは何か？

といった説明には

系統立てた整理を行うことにより、より効率的にデータを扱うことができます。

データを系統立てて扱うために、多くの方法が存在します。 

とあります。

さて、何を言っているか分かりますか？？

以前、0 or 1で表せない選択肢には、文字列を使うと便利、といった話を書きました。

基本的にはプログラミング言語を扱うときにアルファベットを使うので、ここでも英語をイメージしてもらいたいのですが

アルファベットを使ったローマ字でも同じ説明ができます。

BO-U-KE-N のように、子音と母音の組み合わせで１つの言葉を作ることも、一種のデータ構造である、という説明をこの本では説明しようとしているんですね。

これもある意味で、系統立てた整理、に該当するという話です。

ただ個人的には、あまり重要なポイントではないかなぁ、という印象をもっています。

文字列が構造化されているのは、何らかの言語を操っている人間であれば説明するまでもなく当然に理解できるからです。

なので、むしろその次にある「おべんとうの時間」のワークにじっくり取り組むことをお勧めします。

こちらのデータ構造の方が、よほど重要です。

ここでは、「集合」という数学の概念と、「論理演算」を学びます。

高校の数学ででてきた「集合」を覚えているでしょうか？？

和集合とかべき集合とか、独特の記号を使って暗号のような式を扱ったあの単元は

頭の中の抽象度を上げなければ理解できなくて苦労した覚えがあります。

当時は、何のために勉強しているのか分かりませんでしたが・・・

モノゴトを分類して整理するために、とても重要な考え方だったんですね。

ここからは

集合や論理演算の概念を知っておくことがなぜ重要なのか？

それとプログラミング学習にどのような関係があるのか？

について説明します。

集合とは要するに、モノの集まり、です。

そして集めたモノのことを「要素」と呼びます。

ここでまた過去の投稿に戻ります。

街づくりのワークショップでは街の本質を捉えていくわけですが、その中で、街の要素とは？

といった話が出てきます。

学校や幼稚園、消防署や図書館

ゲームセンターや映画館、東京タワーや温泉、スーパーや商店街、バスや電車・・・

などなどです。

これら一つ一つが、街の要素であり、これらの要素が集まって街となります。

つまり、街とは何か？

と問われたときに、その要素を挙げることで説明することができるのです。

これは、検索条件を指定すること、と言い換えることもできます。

街には学校があって、消防署があって、道路があって、そうそう車が走っていて

線路もある、あ、踏切も！

といった感じでしょうか。

街という集合はかなり大きいので、公共施設とか、交通機関とか

もっと小さな集合に分けて整理する方が良さそうです。

子どもの年齢によっては、街、という大きな単位だと概念としてうまく捉えられないかもしれないので

乗り物、建物、などで集合を作った上で、それを包含するものが街

と説明した方が伝わるかもしれません。

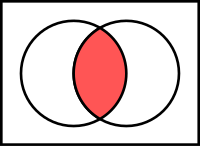
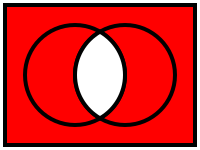
次に「論理演算」ですが、ベン図というものを覚えていますか？？

以下はWikipediaからの抜粋です。

論理和（OR）

論理積（AND）

論理和の否定（NOR）

論理積の否定（NAND）

排他的論理和（XOR）

このように論理演算を使うと、集合を論理的に組み合わせて意味のあるまとまりを作ることができるんですね。

これはつまり

新しい集合を作って適切な名前をつける

ということです。

私たちは日々、無意識のうちにこうした論理集合を頭の中で作っています。

「かつ（AND）」とか「または（OR）」とか「そうではなくて（NOT）」といった組み合わせは日常的に使っていますよね。

モノゴトを定義するときに、この論理集合の考え方は非常に重要です。

適切に分類してモノゴトを整理すれば、曖昧なモノゴトも分かりやすく、間違いなく定義することができるのです。

そう、ルビィから頼まれたペンギンたちが一発で宝石を探し当てたように。

これがつまり

効率的にデータを扱う

です。

やみくもに広い範囲を検索するよりも

論理演算を使ってデータを整理し、可能な限り範囲を絞った方が、効率よく目的に近づくことができます。

これはANDだけでなく、例えばNOTを使って対象から除外する条件を指定することも同じです。

後半のワークには

野菜ANDみどりのもの

といったベン図が出てきます。

野菜といえば、キュウリ、トマト、玉ねぎ、キャベツ…

この中で緑色の野菜といえば…

このベン図はとても便利なので、何かにつけてモノゴトを整理・分類するときに使うと、自然と思考力が身につきますし

さらに、円と円それぞれや、重なったところ、円の外、のようなエリアに対して

名前をつける練習をすると、的確に抽象化するとても良いトレーニングになります。

おべんとう箱の例でいえば

野菜ANDみどりのもの

は、緑黄色野菜、とか。

ここまでは、モノを分類するために集合を使いましたが

ルビィのぼうけんの中では、もう一つ違った使い方をしていることに気づいたでしょうか？

ルビィはこの章の中で

モノ自体を集合と捉え、その特性を要素として抽出する

ということをやっています。

さて、それはどこの部分でしょう？

続きは次回。